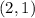Question

What are the coordinates of the turning point for the function f(x) = (x − 2)^3 + 1?

A. (−2, −1)
B. (−2, 1)
C. (2, −1)
D. (2, 1)

Answer 1

The turning point is (2,1).

Hope this helps!

Answer 2

`(2,1)`

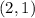
Explanation:

The given function is,

`f(x) = (x -2)^3 + 1`

Turning point of a graph is the point where the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising).

For a cubic function, the critical point also serves as a turning point.

`\Rightarrow f(x) = (x -2)^3 + 1`

`\Rightarrow f'(x) = 3(x -2)^2`

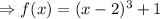
For critical point,

`\Rightarrow f'(x)=0`

`\Rightarrow 3(x -2)^2=0`

`\Rightarrow (x -2)^2=0`

`\Rightarrow x -2=0`

`\Rightarrow x=2`

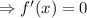
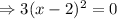
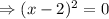
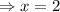
Then,
`f(2) = (2 -2)^3 + 1=1`

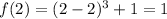
So the critical point or turning point is
`(2,1)`