Question

At what rate is a rider descending when she is 57 feet above ground level?

Answer 1

We have a Ferris wheel with radius r = 38 ft.

It takes 5 minutes to complete a revolution, so we can calculate the tangent speed as:

`\begin{gathered} v=(C)/(t) \\ v=(2\pi r)/(t) \\ v=(2\pi\cdot38ft)/(5\min)\cdot((1\min )/(60s)) \\ v\approx0.795870(ft)/(s) \end{gathered}`

We calculate the module of this speed as the distance travelled in one revolution (one circumference) divided by the time it takes to make that one revolution.

If we consider that the center of the wheel is 38 ft above the ground (that means that the bottom part of the wheel is at ground level), then 57 ft is a height that is 1.5 times the ratio.

Then, we have to find the angle from the center at which y = 57 ftis located:

We can relate h = 19 with the radius r = 38 and the angle α as:

`\begin{gathered} h=r\cdot\sin \alpha \\ \sin \alpha=(h)/(r)=(19)/(38)=0.5 \\ \alpha=\arcsin (0.5)=30\degree \end{gathered}`

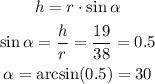
Then, we know that the angle is 30°.

Then, if we draw the components of the speed, we get:

We are only interested in the vertical component, so we can use the graph to relate Vy to the module of the speed and the angle we have already calculated:

`\begin{gathered} V_y=v\cdot\cos (\alpha) \\ V_y=0.795870\cdot\cos (30\degree) \\ V_y\approx0.795870\cdot0.866025 \\ V_y\approx0.689 \end{gathered}`

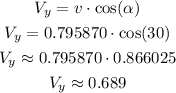
Answer: she is descending at a rate of 0.689 ft/s.