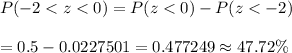Answer:
Explanation:
We assume the population of grades on history exams is known to be normally distributed.
Given : Population mean :
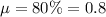
Standard deviation :
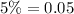
Let x be the random variable that represents the grades on history exams .
Z-score :
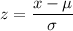
For x= 0.70
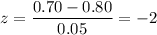
For x=0.80
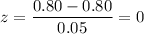
By using the standard normal distribution table , the probability of students earn a score between 70% and 80% will be :_