Question

How long would it take for a sound impulse to travel through a copper rod 25 kilometers long? the speed of copper is 3,500

0.071 sec
0.14 sec
7.1 sec
140 sec

Answer 1

7.1 sec

Step-by-step explanation:

v=d/t or t=d/v

Answer 2

7.1 sec

Step-by-step explanation:

The speed of sound in copper is

`v=3500 m/s`

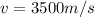
The lenght of the rod, which is the distance the sound wave should travel, is

`S=25 km=25,000 m`

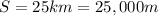
We know that the relationship between distance traveled, speed and time taken is:

`v=(S)/(t)`

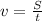
where t is the time taken. By re-arranging the equation and using the data of the problem, we find the time the sound wave takes to travel through the rod:

`t=(S)/(v)=(25,000 m)/(3500 m/s)=7.1 s`