Question

Would the inverse of this graph be a function? Why or why not?

Answer 1

We will have the following:

*First: We would determine the piecewise function that describes the graph.

Since we can see that the function increases by a factor of 2 and decreases by the same factor we would have:

`f(x)=\begin{cases}2x\colon x\ge0\land x\le4 \\ \\ -2x+16\colon x>4\land\le8\end{cases}`

This is:

*Second: We calculate the inverse of the piecewise function:

`f^(-1)(x)=\begin{cases}(x)/(2)\colon x\ge0\land x\le4 \\ \\ -(x-16)/(2)\colon x>4\land x\le8\end{cases}`

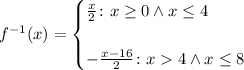
That is:

From this we can see that the inverse of that graph would in fact represent a function, a non-continuous function. [It will represent a function as long as it follows the parameters stablished in the first point]