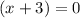Question

If (x+1)(x-3)=12, then which of the following statements is true?

A. X+1=0 or x-3=0
B. X+1=12 or x-3=12
C. X-5=0 or X+3=0

Answer 1

C.
`(x-5)=0, (x+3)=0`

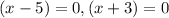
Explanation:

To solve the quadratic equation we need it to be equal to zero:

`(x+1)(x-3)=12\\x^2-3x+x-3=12\\x^2-3x+x-3-12=0\\x^2-3x+x-15=0`

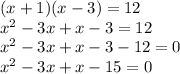
Now we factor the expression by putting in each parenthesis the square root of
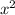`x^2` wich is
`x`. And we look for two numbers that when multiplied give -15 and when added they result in -2

Those numbers are -5 and +3

The factorization is as follows:

`(x-5)(x+3)=0`

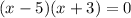
When we have something equal to zero, we have the options that either one of the two elements is equal to zero, or even both can be equal to zero, for this property, the above gives us the solutions:

`(x-5)=0`

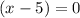
and

`(x+3)=0`

Answer 2

C. x-5=0 or x+3=0

Explanation:

Given,

`(x+1)(x-3)=12`

`x^2+1x-3x-3=12` ( By multiplication )

`x^2-2x-3=12` ( By operating like terms )

`x^2-2x-3-12=0` ( Subtracting 12 on both sides )

`x^2-2x-15=0`

`x^2-5x+3x-15=0` ( By middle term splitting )

`x(x-5)+3(x-5)=0`

`(x+3)(x-5)=0`

By the zero product property,

`(x+3)=0\text{ or }(x-5) =0`

Hence, option C is correct.