Question

How fast is a car moving, and in which direction, if the frequency of the horn drops from 900 Hz to 875 Hz as heard by a stationary listener? Assume T = 0oC.

Answer 1

The initial frequency of sound from the source is f = 900 Hz.

The final frequency of sound from the source heard by the observer is f' = 875 Hz.

As the frequency of sound is decreasing, thus, the source is moving away from the observer.

Hence, the car is moving away from the observer.

By Doppler's effect, the speed of the car is,

`f^(\prime)=f(\frac{v}{v+v_s_{}})`

where v is the speed of the sound and v_s is the speed of the source,

The speed of the sound in 0 degrees celsius is,

`v=344\text{ m/s}`

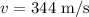
Substituting the known values,

`\begin{gathered} 875=900*((344)/(344+v_s)) \\ 875=(309600)/(344+v_s) \end{gathered}`

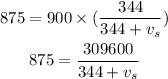
By cross multiplication,

`\begin{gathered} 875*(344+v_s)=309600 \\ 301000+875v_s=309600 \\ 875v_s=309600-301000 \\ 875v_s=8600 \end{gathered}`

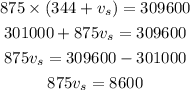
By simplifying,

`\begin{gathered} v_s=(8600)/(875) \\ v_s=9.83\text{ m/s} \end{gathered}`

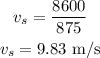
Thus, the speed of the car is 9.83 meters per second.