Given: It is given that
 and
and
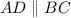 .
.
To Prove: ABCD is a parallelogram.
Statements
1.
 and
and
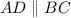
Reason: Given
2.
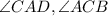 are alternate interior angles
are alternate interior angles
Reason: Def of alternate interior angles
3.

Reason: Alternate interior angles are congruent
4.

Reason: Reflexive property
5.
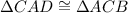
Reason: SAS congruency theorem
6.
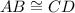
Reason: Corresponding Parts of Congruent triangles are Congruent (CPCTC)
7. ABCD is a parallelogram
Reason: Parallelogram Side Theorem