Question

Which number comes next in this series? 1/64, 1/32, 1/16, 1/8, 1/4, 1/2, ?

Answer 1

This is a geometric sequence, with the first term: 1/64

The common ratio is found through the ratio of the first two terms and the second and third term.

`((1)/(32))/((1)/(64)) = ((1)/(16))/((1)/(32))`

`(1)/(32) \cdot 64 = (1)/(16) \cdot 32`

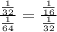
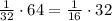
Since there is a common difference of 2, we can generalise this sequence to find the nth term:

`T_n = ar^(n-1)`
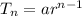
a is the first term, r is the common ratio, and n is the nth term in the sequence.


`T_n = (1)/(64) \cdot 2^(n-1)`
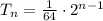
Substituting n = 7, we get:

`T_7 = (1)/(64) \cdot 2^(7 - 1)`

`T_7 = (1)/(64) \cdot 64`

`T_7 = (64)/(64) = 1`

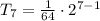
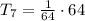
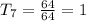
Thus, the next term in the sequence is 1.