Question

Assume that you have an ordinary deck of 52 playing cards. how many possible 7-card poker hands are there that contain exactly one ace and one king?

Answer 1

Let's deal with the restrictions first.
To get one ace, we have 4 total aces, and we want to choose one ace:

`\text{One ace: } ^(4)C_1`

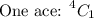
We can repeat this for the king, as well.

`\text{One king: } ^(4)C_1`

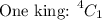
Now, let's deal with the remaining five cards.
Since we can't deal a king or an ace anymore, let's subtract 8 from a pack of 52. This ensures that we don't pick a king or an ace anymore.

Now, we simply need to pick five cards from a pack of 44 cards:

`\text{Five cards: } ^(44)C_5`

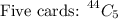
Thus, the total number of ways to pick exactly one ace and one king is:

`^(4)C_1 \cdot ^(4)C_1 \cdot ^(44)C_5`

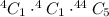
The calculator should do the rest.