Question

The excluded values of a rational expression are –3, 0, and 8. Which of the following could be this expression?

x+2/x^3-5x^2-24x

x+2/x^2-5x-24

x^3-5x^2-24x

x^2-5x-24/x+2

Answer 1

It has to be the first expression because that is the only expression that has an x^3 in the denominator. An x^3 in the denominator is what causes the 3 excluded values.

Answer 2

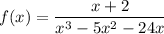`f(x)=(x+2)/(x^3-5x^2-24x)` has denominator
`x^3-5x^2-24x`

Option 1 is correct.

Explanation:

Given: The excluded values of a rational expression are –3, 0, and 8

The excluded value of any function is vertical asymptotes.

We get vertical asymptotes when denominator becomes 0.

If we find a function of excluded value it must we equivalent to denominator of function.

Function of excluded value, (x+3)(x-0)(x-8)

Now we will simplify it

`\Rightarrow x(x^2-5x-24)`

`\Rightarrow x^3-5x^2-24x`

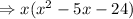
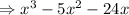
Now, we will check each option those has denominator
`\Rightarrow x^3-5x^2-24x`

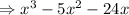
Hence, Option 1
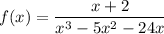`f(x)=(x+2)/(x^3-5x^2-24x)` has denominator
`x^3-5x^2-24x`