Question

I need help with this problem

Answer 1

Fourth Choice

Explanation:

To answer this, we will start by using the Midpoint Theorem, which states that the segment that connects the midpoints of two sides of a triangle is parallel to the third side.

In this case, since D is midpont of AB and E is midpoint of BC, DE is parallel to AC.

Because they are parallel, the angles ∠BED and ∠BCA are corresponding angles and so are the angles ∠BDE and ∠BAC. Also, the angles ∠ABC and ∠DBC are the same, so:

∠BED=∠BCA

∠BDE=∠BAC

∠ABC= ∠DBC

Thus the triangles ΔABC and ΔBDE are similar.

This means that:

`(BC)/(BE)=(BA)/(BD)=(AC)/(DE)=k`

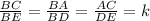
We can calculate k using BE and BC:

`(BC)/(BE)=k`

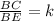
Since E is midpoint of BC, BC = 2*BE, so:

`(BC)/(BE)=k`

`(2xBE)/(BE)=k`

`2=k\\ k=2`

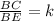
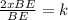
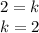
Now, we can use the relation of DE, AC and k to calculate AC:

`(AC)/(DE)=k=2\\ AC=2xDE\\ AC=2x3\\ AC=6`

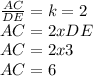
This corresponds to the fourth alternative.

Answer 2

as you see from B to E it's 2 and from E to D is 3 so it can only be 4 or 6. if it was 4 it would br a Lil bigger not a whole lot bigger so I would say 6 because it's bigger than it would be of it was 4..!!!??