Question

Great Dish believes that it will need new equipment in 8 years. The equipment will cost $26,000. What lump sum should be invested today at 12%, compounded semiannually, to yield $26,000?

Answer 1

A=p (1+I/k)^tk
26000=p (1+0.12/2)^(2×8)
Solve for p
P=26,000÷(1+0.12÷2)^(2×8)
P=10,234.80

Answer 2

$ 10,234.80 should be invested.

Explanation:

Since, the amount formula in compound interest,

`A=P(1+(r)/(n))^(nt)`

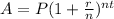
Where, P is the principal amount,

r is the annual rate,

n is the number of period in a year,

t is the number of years,

Here, A = $ 26,000, r = 12% = 0.12, t = 8 years,

n = 2 ( number of semiannual in a year = 2 ),

By substituting the values,

`26000=P(1+(0.12)/(2))^(2* 8)`

`26000=P(1+0.06)^(16)`

`\implies P=(26000)/((1.06)^(16))=10234.8033765\approx 10234.80`

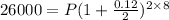
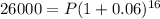
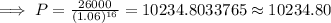
Hence, $ 10,234.80 should be invested.