Answer with Explanation:
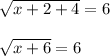
Squaring Both sides
→x + 6 =36
→x +6 -6=36-6
→x=30
When we substitute , x=30 in the original equation ,we get
L H S
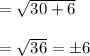
One value is 6 and other is ,-6.
So, x=30, is not an extraneous solution.
→→Secondly if your equation is
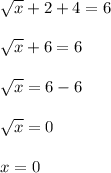
Substituting ,the value of x, in original equation
L H S
= 0 +2 +4
=6
=R HS
So, x=0, is also not an extraneous solution.
Or, if the equation is
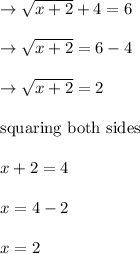
Substituting the value of ,x in original equation
LHS
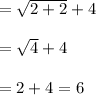
=RHS
So, x=2 , is not an Extraneous Solution.