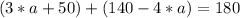Question

Given that ∠XQR = 180° and ∠LQM = 180°, which equation could be used to solve problems involving the relationships between ∠MQR and ∠LQR?

A) (3a + 50) + 180 = (140 − 4a)
B) (3a + 50) + (140 − 4a) = 180
C) (140 − 4a) − 180 = (3a + 50)
D) (3a + 50) − (140 − 4a) = 180

Answer 1

The answer is B, when you add ∠MQR and ∠LQR you will get 180°.

Answer 2

The answer is B

Explanation:

In order to determine the equation, we have to know some properties about the addition of angles.

As the angles ∠XQR and ∠ LQM are 180°, they form straight lines. When two straight lines intercept each other, the angles opposite each other are equal.

The property is called "Vertically Opposite Angles".

Also, we know that ∠ LQM=180°, so it is the same that:

`(140-4*a)+(3*a+50)=180`

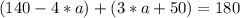
Therefore, the relationship between ∠MQR and ∠LQR is:

C.
`(3*a+50)+(140-4*a)=180`