Question

The area of an isosceles trapezoid is 72m2 and its diagonals are perpendicular. Find the length of a diagonal.

Answer 1

In an isosceles trapezoid, when the diagonals are perpendicular the area = h^2. So, h = sqrt(72) = 8.49

The length of a diagonal of a square is (x)sqrt(2)
x = 8.49
The length of the diagonal is (8.49)sqrt(2) = 12

Answer 2

12 meters.

Explanation:

Let h represent the length of each diagonal of the given isosceles trapezoid.

We have been given that the area of an isosceles trapezoid is
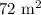`72\text{ m}^2` and its diagonals are perpendicular.

We know that area of a trapezoid with perpendicular diagonals is equal to half the product of diagonals.
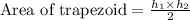`\text{Area of trapezoid}=(h_1* h_2)/(2)`, where,

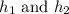`h_1\text{ and } h_2` represents diagonals of trapezoid.

Since both diagonals of isosceles trapezoid are congruent, so our formula would be:

`\text{Area of trapezoid}=(h* h)/(2)`

`72\text{ m}^2=(h^2)/(2)`

`2*72\text{ m}^2=(h^2)/(2)*2`

`144\text{ m}^2=h^2`

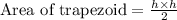
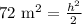
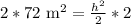
Upon taking square root of both sides of our equation we will get,

`\sqrt{144\text{ m}^2}=h`

`12\text{ m}=h`

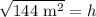
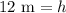
Therefore, the length of each diagonal of our given trapezoid is 12 meters.