Question

A player bounces a basketball on the floor, compressing it to 80.0 % of its original volume. The air (assume it is essentially N2 gas) inside the ball is originally at a temperature of 20.0 ∘C and a pressure of 2.00 atm. The ball's diameter is 23.9 cm. By how much does the internal energy of the air change between the ball's original state and the maximum compression?

Answer 1

Answer: 292.95 J

Step-by-step explanation:

change in internal energy= Heat transfer - work done

ΔU =Q -PΔV

Here, Q = 0 as there is no heat transfer.

P =2.00 atm = 2.00 × 101235 Pa = 202470 Pa

ΔV = final volume - initial volume = 0.8 V -V = -0.2 V

where V is the initial volume.

Volume of a spherical ball,
`V = (4)/(3)\pi r^3`

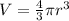
r = d/2 = 23.9 cm / 2 = 0.12 m

`V = (4)/(3)* 3.14 * (0.12m)^3= 7.23*10^(-3)m^3`

`\DeltaU = -P\DeltaV = - 202470 Pa * -0.2 * 7.23*10^(-3)m^3=292.95 J`

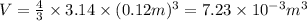
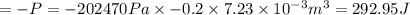
Hence, internal energy would change by 292.95 J.