Question

Which is equivalent to 16^3/4x

Answer 1

The given expression is equivalent to
`(\sqrt[4]{16})^(3x)` or
`8^x`.

Explanation:

The given expression is

`16^{(3)/(4)x}`

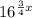
Use the property of exponent ,

`x^(mn)=(x^m)^n`

`16^{(3)/(4)x}=(16^(1)/(4))^(3x)`

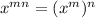
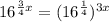
Use the property of radical expression,

`x^{(1)/(n)}=\sqrt[n]{x}`

`16^{(3)/(4)x}=(\sqrt[4]{16})^(3x)`

Therefore the given expression is equivalent to
`(\sqrt[4]{16})^(3x)`.

After more simplification we get,

`16^{(3)/(4)x}=2^(3x)`

`16^{(3)/(4)x}=8^x`

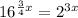
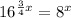
Therefore the given expression is also equivalent to
`8^x`.

Answer 2

I used a photo to reduce confusion. When solving fractional indices, the numerator becomes the power and the denominator becomes the root. Hope this helps.