Question

let a,b,c,d be four integers (not necessarily distinct) in the set {1,2,3,4,5}. the no. of polynomials x^4+ax^3+bx^2+cx+d which is divisible by x+1 is

Answer 1

By either long or synthetic division, it's easy to show that


`(x^4+ax^3+bx^2+cx+d)/(x+1)=x^3+(a-1)x^2+(-a+b+1)x+(a-b+c-1)-(a-b+c-d-1)/(x+1)`

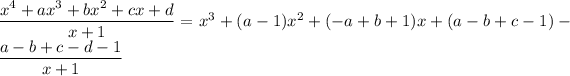
The quartic will be exactly divisible by
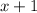
`x+1` when the numerator of the remainder term vanishes, or for those values of
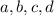
`a,b,c,d` such that


`a-b+c-d-1=0`

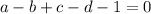
I'm not sure how to count the number of solutions (software tells me it should be 80), but hopefully this is a helpful push in the right direction.