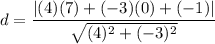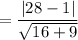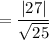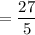Answer-
The corresponding height of the parallelogram is
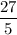 units
units
Solution-
Hint- The perpendicular distance between the point S and the straight line RU is the length of the height of the parallelogram.
Equation of RU-
Applying two point formula between (4, 5), (1, 1)
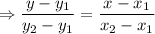
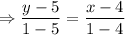
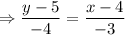
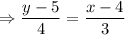
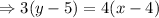
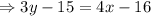
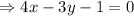
Perpendicular distance between S and RU-
The distance d from a point (x₀, y₀) to the line ax+by+c=0 is
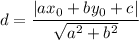
Distance of (7, 0) from line
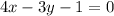 is,
is,