Question

Solve:
nC6 = nC4

Need help, I don't want to expand. Is there a shortcut method?

Answer 1

Yes, there is.
Of course, the longer way is to formulate the combinations formula, but we need to understand what nCr actually represent in order to understand the shortcut.

For a binomial expansion (1 + x)ⁿ, we always have nC0, nC1, etc. at the start of each term because they represent coefficients of a binomial expansion. This is the core foundation of a binomial expansion. However, using this property, we also know that for a binomial expansion, there lies another property:

the Binomial coefficient symmetry:
This is a property in every binomial expansion, and we can see this if we were to expand the (1 + x)ⁿ from n = 1 to n = 3. This rule shows that, from the middle term, each term before and after it is equal. Let's use this rule to demonstrate the property:


`(1 + x)^(2) = \boxed{1} \cdot 1 + 2x + \boxed{1} \cdot x^(2)`

`(1 + x)^(3) = 1 \cdot 1 + 3x + 3x^(2) + 1 \cdot x^(3)`

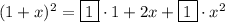
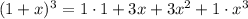
In this case, we have an even number of terms, and thus, the middle coefficient is hidden as 0. This still applies.

So, we can conclude:

`^(n)C_r = ^(n)C_(n - r)`

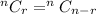
Using this:

`^(n)C_6 = ^(n)C_(n - 6) = ^(n)C_4`
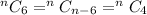
So, n - 6 = 4
and n = 10.