Question

Given that triangle QRS is similar to triangle DEF, what is x?

x= 9.8
x= 15.6
x= 23.7
x= 20.5

Answer 1

So the ratio is 40/26 = 1.54

24 ÷ 1.54 = 15.58

2x-4 = 15.58

2x = 19.58

x = 9.8

Answer 2

x = 9.8

Explanation:

Given that triangle QRS is similar to triangle DEF.

Hence, the ratio of corresponding sides of these triangles are equal.

Thus, we have

`(QR)/(DE)=(RT)/(EB)`

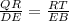
Substituting the known values from the given figure

`(26)/(40)=(2x-4)/(24)`

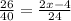
Cross multiplying, we get

`40(2x-4)=26\cdot24\\\\80x-160=624\\\\80x=784\\\\x=(784)/(80)\\\\x=9.8`

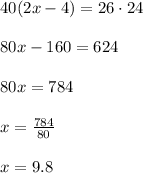
The value of x is 9.8