Question

What is the length of the Midsegment?
12
18
6
9

Answer 1

The length of Midsegment = 9

Explanation:

the midsegment connecting the midpoints of two sides of a triangle is parallel to the third side of the triangle, and the length of this midsegment is half the length of the third side.

According to the Midsegment Theorem:

• The midsegment connects the midpoints of two sides of a triangle is parallel to the third side of the triangle.

• The length of this midsegment is half the length of the third side.

Thus,

The midsegment (x+4) is half the length of the third side (4x-2). so

`\left(x+4\right)\:=\:(1)/(2)\:\left(4x\:-\:2\right)`

`x+4=2x-1`

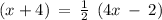
Subtract 4 from both sides

`x+4-4=2x-1-4`

`x=2x-5`

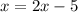
Subtract 2x from both sides

`x-2x=2x-5-2x`

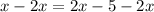
Simplify

`-x=-5`

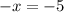
divide both sides by -1

`(-x)/(-1)=(-5)/(-1)`

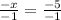
Simplify

`x=5`

As

The length of Midsegment = x+4

= (5) + 4 ∵ x = 5

= 9

Therefore, the length of Midsegment = 9