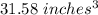Question

IN NEED OF A MATH WIZ!!!!!

A cylindrical canister contains 3 tennis balls. Its height is 7 inches, and its radius is 1.5 inches. The diameter of one tennis ball is 2.25 inches. How much of the canister’s volume is unoccupied by tennis balls? Use 3.14 for π, and round your answer to the nearest hundredths place.

31.58 in3
3 49.46 in3
3 5.96 in3
3 17.88 in3

Answer 1

The unoccupied volume will be the volume of the can minus the volume of the three tennis balls.

V=HπR^2-3(4πr^3)/3

V=HπR^2-4πr^3 where H=height of can, R=radius of can, r=radius of ball

We are told H=7, R=1.5, and r=1.125 (2.25/2=d/2=r) so

V=7π1.5^2-4π1.125^3

V=15.75π-5.6953125π in^3

V≈31.58 in^3

Answer 2

Answer:
`31.58\ inches^3`

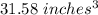
Explanation:

Given: The diameter of tennis ball = 2.25 inches

The radius of ball =
`(2.25)/(2)=1.125\ inches`

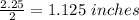
The volume of ball (sphere) is given by :-

`V=(4)/(3)\pi r^3\\\\\Rightarrow V=(4)/(3)(3.14)(1.125)^3\\\\\Rightarrow\ V=5.96109375\approx5.96\ inch^3`

For cylindrical canister, Height = 7 inches

Radius = 1.5 inches

The volume of cylindrical canister (cylinder) is given by :-

`V=\pi r^2h\\\\\Rightarrow V=(3.14)(1.5)^2(7)\\\\\Rightarrow\ V=49.455\approx49.46\ inch^3`

Now, the canister’s volume is unoccupied by tennis balls

= Volume of canister - volume of 3 balls

=
`49.46-3(5.96)=49.46-17.88=31.58\ inches^3`

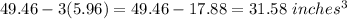
Hence, the canister’s volume is unoccupied by tennis balls=
`31.58\ inches^3`