Question

*PLEASE HELP! 27 POINTS!!! **

The line of best fit for a scatter plot is shown:

1. A scatter plot and line of best fit are shown. Data points are located at 0 and 1, 2 and 1, 2 and 3, 4 and 3, 4 and 5, 6 and 3, 7 and 5, 9 and 4. A line of best fit passes through the y-axis at 1 and through the point 4 and 3.

What is the equation of this line of best fit in slope-intercept form?

y = 1x + one half

y = one half x + 1

y = 1x − one half

y = negative one half x + 1

2. A graph shows the survey results for a group of students who were asked how many honors classes they have taken and how many elective classes:

A scatter plot is shown with the title class choices. The x axis is labeled number of honors classes and the y axis is labeled number of electives. Data points are located at 1 and 8, 3 and 6, 3 and 9, 5 and 3, 6 and 6, 6 and 9, 8 and 6. A line of best fit crosses the y axis at 9 and passes through the point 6 and 6.

How many elective classes would students likely have taken if they have taken 12 honors classes?

15, because y = one halfx + 9

12, because y = y = negative one halfx + 9

6, y = ˜one halfx + 9

3, because y = negative one halfx + 9

Answer 1

1.) Y= one half x + one
2.) 3 because Y= negative one half x +9

Answer 2

1)

`y=(1)/(2)* x+1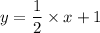` i.e. y = one half x + 1

2)

3, because y = negative one halfx + 9

Explanation:

1)

It is given that the line of best fit of the scatter plot passes through the points (0,1) and (4,3).

so we will find the equation of line of best fit.

We know that the equation of line passing through two points (a,b) and (c,d) is calculated as:

`y-b=(d-b)/(c-a)* (x-a)`

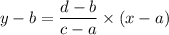
Here we have:

(a,b)=(0,1) and (c,d)=(4,3).

Hence, the equation of line is:

`y-1=(3-1)/(4-0)* (x-0)\\\\y-1=(2)/(4)* x\\\\y=(1)/(2)* x+1`

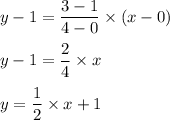
Hence, the equation of this line of best fit in slope-intercept form is:

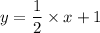`y=(1)/(2)* x+1` i.e. y = one half x + 1

2)

It is given that the line of best fit crosses the y axis at 9 and passes through the point 6 and 6 i.e. it passes through (0,9) and (6,6).

so we will find the equation of line of best fit.

We know that the equation of line passing through two points (a,b) and (c,d) is calculated as:

`y-b=(d-b)/(c-a)* (x-a)`

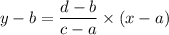
Here we have:

(a,b)=(0,9) and (c,d)=(6,6).

Hence, the equation of line is:

`y-9=(6-9)/(6-0)* (x-0)\\\\y-9=(-3)/(6)* x\\\\y=(-1)/(2)* x+9`

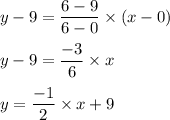
Hence, the equation of this line of best fit in slope-intercept form is:

`y=(-1)/(2)* x+9`

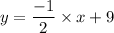
Now we are asked to find the value of y when x=12.

`y=(-1)/(2)* 12+9\\\\y=-6+9\\\\y=3`

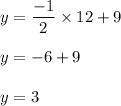
Hence, the correct answer is:

3, because y = negative one halfx + 9