The given information is:
![\sin \theta=\frac{3}{\sqrt[]{15}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/1d9ws29rdbegqb8pj3p6.png)
And angle theta is in quadrant I, then know that:
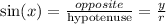
Then y=3 and r=square root (15)
By the Pythagorean theorem we can find x:
![\begin{gathered} r^2=x^2+y^2 \\ x^2=r^2-y^2 \\ x=\sqrt[]{r^2-y^2} \\ x=\sqrt[]{(\sqrt[]{15})^2-3^2} \\ x=\sqrt[]{15-9} \\ x=\sqrt[]{6} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wcm7tcpj0nwaoe64cdi8.png)
And the tangent is:
![\begin{gathered} \tan (x)=(y)/(x) \\ \tan \theta=\frac{3}{\sqrt[]{6}} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/cqz2ueopn5ru9rxp0say.png)
Thus, tan 2theta:
![\begin{gathered} \tan 2\theta=(2\tan\theta)/(1-\tan^2\theta) \\ \tan 2\theta=\frac{2\frac{3}{\sqrt[]{6}}}{1-(\frac{3}{\sqrt[]{6}})^2} \\ \tan 2\theta=\frac{\frac{6}{\sqrt[]{6}}}{1-(9)/(6)} \\ \tan 2\theta=\frac{\frac{6}{\sqrt[]{6}}}{-(3)/(6)} \\ \tan 2\theta=\frac{\frac{6}{\sqrt[]{6}}}{-(1)/(2)} \\ \tan 2\theta=\frac{6\cdot2}{-1\cdot\sqrt[]{6}} \\ \tan 2\theta=\frac{12}{-\sqrt[]{6}} \\ \tan 2\theta=-\frac{12}{\sqrt[]{6}} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/nx5ot1p6va6h5x8s5z3b.png)
Then the exact value of tan 2theta in simplest radical form is -12/square root(6)