Answer:
The two triangles are similar by SAS postulate of similarity ⇒ A
Explanation:
Let us revise the cases of similarity
- AAA similarity: two triangles are similar if all three angles in the first triangle equal the corresponding angle in the second triangle
- AA similarity: If two angles of one triangle are equal to the corresponding angles of the other triangle, then the two triangles are similar.
- SSS similarity: If the corresponding sides of the two triangles are proportional, then the two triangles are similar.
- SAS similarity: In two triangles, if two sets of corresponding sides are proportional and the included angles are equal then the two triangles are similar.
In the given figure
∵ There are 2 triangles
∵ The ratio between 2 corresponding sides in the Δs is
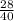
∵
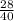 = 0.7
= 0.7
∵ The ratio between the other 2 corresponding sides in the Δs is
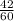
∵
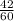 = 0.7
= 0.7
→ That means 2 sets of corresponding sides have an equal ratio
∴ The 2 sets of corresponding sides are proportional
→ By using the parallel sides
∵ There are two parallel sides
∴ The angles between the sides 28, 42, and the sides 40, 60 equal
because they are corresponding angles
∴ The included angles are equal in measures
→ By using case 4 above
∴ The two triangles are similar by SAS postulate of similarity