Answer:
A. Equation: V(t) = -3500t + 62 000
B. $23,500
Explanation:
We are told that the price of the car can be modelled as a linear equation. This means, we can write

where m is the slope of the line and b is the y-intercept.
Now we know that the points (0, 62 000) and (6, 41 000) lie on the line. Therefore, the slope of the line is
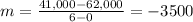
Therefore, the equation thus far we have is
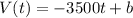
Now what is the y-intercept b? the y-intercept is found by putting t = 0 into the equation. Luckily for us though, we know that the point (0, 62,000) lies on the line. This tells us that b = 62,000. Therefore, the equation of the line is

Part B.
Now that we have the equation that models the price of the car, we can find the price after 11 years by putting t = 11 into the above equation. This gives

The right hand simplifies to give
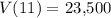
which is our answer!