Question

What is the equation of the parabola shown in the graph?

A.    y = -x^2/8 - x - 4

B.    y = -x^2/4 - 2x - 8

C.    y = -x^2/4 - 2x - 7

D.    y = -x^2/8 - x - 5

Answer 1

c is the correct answer

Answer 2

Option C

Explanation:

The standard form is (x - h)2 = 4p (y - k), where the focus is (h, k + p) and the directrix is y = k - p.

The focus is -4,-4 and the directrix is y=-2 therefore h=-4 and

-2=k-p and -4=k+p adding this last equations we get -6=2k therefor k=-3

and p=-1

we plug this in the equation of the standard form we get:

`(x+4)^(2) =-4(y+3)`

`x^(2) +8x+16=-4y-12`

`x^(2) +8x+28=-4y`

`-(x^(2))/(4)  -2x-7=y`

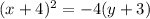
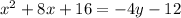
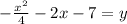
Option C