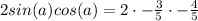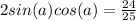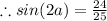Since a is in the third quadrant, both sina and cosa are negative.
Now, sin(2a) can be rewritten as 2sin(a)cos(a).
Thus, we can find sin(a) by using Pythagoras' Theorem.

Now, by focusing on the positive value, we can see that 5 is the hypotenuse.
Let the missing side be x.
x² + 16 = 25
x² = 9
x = 3, because x > 0
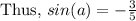
Substituting these into the equation, we get: