Question

Determine whether a triangle can be formed with the given side lengths. If so, use Heron's formula to find the area of the triangle. a = 240 b = 121 c = 302

Answer 1

The area of triangle formed by given side lengths is 13724.27.

Explanation:

A triangle can be formed If the sum of the other two sides (except largest side) is greater than the largest side that is a+b>c.

Here, given side lengths:

a = 240

b = 121

c = 302

Here, largest side is c = 302

so taking sum of other two sides,

a+b = 240+121 = 361> 302

Hence, triangle can be formed with a, b and c as given lengths.

Calculating area using Heron's formula,

`Area=√(s(s-a)(s-b)(s-c))`

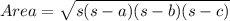
where s is the semi perimeter

Formula to find semi perimeter is

`s=(a+b+c)/(2)`

So, first we find the semi perimeter by using given sides,

`s=(240+121+302)/(2)`

`s=(663)/(2)`

`s=331.5`

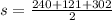
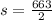
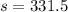
Now put the value of s,a,b and c in the Heron's formula,

`Area=√(s(s-a)(s-b)(s-c))`

`Area=√(331.5(331.5-240)(331.5-121)(331.5-302))`

`Area=√(331.5*91.5*210.5*29.5)`

`Area=√(188355689.438)`

`Area=13724.2737308`

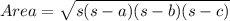
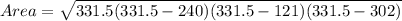
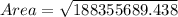
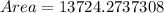
Therefore, the area of triangle is approx. 13724.27.