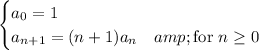Let
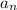
denote the factorial of any non-negative integer

.
By convention, we take
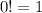
, so that
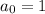
. As
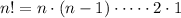
by definition, we can obtain the next integer's factorial,
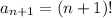
, by multiplying the previous term
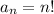
by the next integer.
The recursive definition for the factorial function can then be given by