Question

A building has a ramp to its front doors to accommodate the handicapped. If the distance from the building to the end of the ramp is 19 feet and the height from the ground to the front doors is 4 feet, how long is the ramp? (Round to the nearest tenth.)

Answer 1

The length of the ramp is 19.4 feet.

Explanation:

Let's draw a figure for the given situation.

Here building end touches the ground forms 90 degrees. So it forms a right triangle.

We use the Pythagorean theorem statement to find the length of the ramp.

The Pythagorean theorem states the sum of the squares of legs is equal to square of the hypotenuse.

`AC^2 = AB^2 + BC^2`

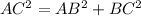
Here AC is the length of the ramp and AB = 4 and BC = 19. Plug in the given values in the above statement, we get

`AC^2 = 4^2 + 19^2\\AC^2 = 16 + 391`

`AC^2 = 377`

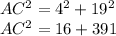
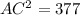
Taking square root on both sides, we get

AC = √377

AC = 19.4 {rounded of to the nearest tenths place]

Therefore, the length of the ramp is 19.4 feet.

Answer 2

ramp² = 19² + 4²
ramp² = 361 + 16
ramp² = 377
ramp = 19.42
***************************************************************************
Incidentally, the angle of the ramp would be
tan (angle) = 4 / 19
tan (angle) = 0.210526315789474
arc tan (0.210526315789474) = 11.889 Degrees