Question

The position of an object at time t is given by s(t) = 7 - 14t. Find the instantaneous velocity at t = 7 by finding the derivative.

Answer 1

Given the position function
s(t) = 7 - 14t

The instantaneous velocity is the derivative the the position function:
s'(t) = v = - 14

The velocity in an instant in time is 14 m/s in the opposite direction.

Answer 2

The velocity of the object is 14m/s in opposite direction for any value of t.

Explanation:

The position of an object at time t is given by

`s(t)=7-14t`

Differentiate with respect to t.

`s'(t)=0-14(1)`

`s'(t)=-14`

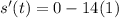
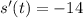
We know that the change in displacement with respect to time is known as velocity.

`v(t)=-14`

Therefore the velocity of the object is 14m/s in opposite direction for any value of t.