
There are three stationary points at

.
When
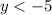
, you have
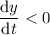
, so

is decreasing here.
When

, you have

, so

is increasing here.
When
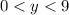
, you have

, so

is increasing here.
When
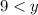
, you have
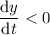
, so

is decreasing here.
To summarize, when

,

will be an increasing function, and this occurs for
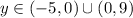
.