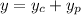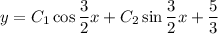Question

Solve 4y'' + 9y = 15 by undetermined coefficients

Answer 1

The homogeneous part of the ODE has characteristic equation


`4y''+9y=0\implies 4r^2+9=0`

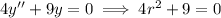
which has roots at
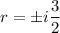
`r=\pm i\frac32`. This means the characteristic solution takes the form


`y_c=C_1\cos\frac32x+C_2\sin\frac32x`

For the particular solution, we can attempt to find a solution of the form


`y_p=a_0`

`\implies {y_p}''=0`

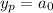
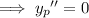
and substituting into the nonhomogeneous ODE, we get


`4(0)+9a_0=15\implies a_0=\frac{15}9=\frac53`

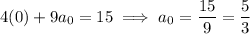
so that the particular solution is


`y_p=\frac53`

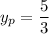
and the general solution to the ODE is


`y=y_c+y_p`

`y=C_1\cos\frac32x+C_2\sin\frac32x+\frac53`