Question

What is the sum of the infinite geometric series?

A. –288
B. –216
C. –144
D. –72

Answer 1

Let
`S_N` denote the
`N`th partial sum of the series. Then


`S_N=\displaystyle\sum_(n=1)^N(-144)\left(\frac12\right)^(n-1)`

`S_N=\displaystyle-144\left(1+\frac12+\frac1{2^2}+\cdots+\frac1{2^(N-1)}+\frac1{2^N}\right)`

Multiplying both sides by
`\frac12` gives


`\frac12S_N=\displaystyle\sum_(n=1)^N(-144)\left(\frac12\right)^n`

`\frac12S_N=\displaystyle-144\left(\frac12+\frac1{2^2}+\frac1{2^3}+\cdots+\frac1{2^N}+\frac1{2^(N+1)}\right)`

Subtracting the last expression from
`S_N`, we have




`\displaystyle\frac12S_N=-144\left(1-\frac1{2^(N+1)}\right)`

`\displaystyle S_N=-288\left(1-\frac1{2^(N+1)}\right)`

As
`N\to\infty`, we end up with the original infinite series. The rational term approaches 0, leaving us with


`\displaystyle\sum_(n=1)^\infty(-144)\left(\frac12\right)^(n-1)=\lim_(n\to\infty)S_N=-288`

so the answer is A.

Answer 2

Option A is correct that is -288

Step-by-step explanation:

Formula for sum of infinite geometric progression
`S_(\infty) =(a)/(1-r)`

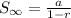
where,

a is the first of geometric series

r is the common ratio of geometric series

here, a= -144 and r=1/2

Now, substituting the values in the formula we will get

`\Rightarrow (-144)/(1-(1)/(2))\\\\\Rightarrow -288`

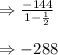
sum of the infinite geometric series= -288

So, Option A is correct that is -288