Answer:
B
Explanation:
The formula for standard deviation is:
St. Dev =
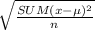
This means "we subtract the mean,
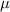 , from each value given in the data set and square the result. Then SUM each of them. Then divide by total number of numbers,
, from each value given in the data set and square the result. Then SUM each of them. Then divide by total number of numbers,
 . Then take the square root of the total."
. Then take the square root of the total."
Finding mean,
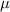 , first:
, first:
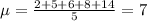
Now calculating St. Dev.:
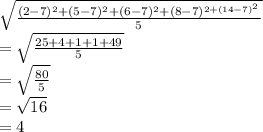
Answer choice B is right.