Question

Choose the polynomial that is written in standard form. xy3 + 4x5y + 10x3 x4y2 + 4x2y + 8x −9x4y2 + 4x3y5 + 10x2 x6y3 + 4x4y8 + x2

Answer 1

I am almost positive that the answer is B. This is because the exponents are decreasing as you go right

Answer 2

`x^4y^2+4x^2y+8x`

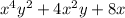
Option 2 is correct.

Explanation:

We need to choose polynomial into standard form.

Standard form of polynomial: The highest degree term should be first one and then write term reducing the exponent.

For example:

`P(x)=ax^n+bx^(n-1)+.......+c`

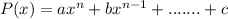
Now, we will see each option for standard polynomial.

Option 1:
`xy^3+4x^5y+10x^3`

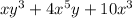
Degree of polynomial = 6

But first term degree is 4

Thus, Not in standard form

Option 2:
`x^4y^2+4x^2y+8x`

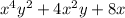
Degree of polynomial = 6

But first term degree is 6

Thus, It is in standard form

Option 3:
`-9x^4y^2+4x^3y^5+10x^2`

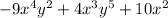
Degree of polynomial = 8

But first term degree is 6

Thus, Not in standard form

Option 4:
`x^6y^3+4x^4y^8+x^2`

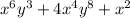
Degree of polynomial = 12

But first term degree is 9

Thus, Not in standard form

Hence,
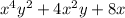`x^4y^2+4x^2y+8x` is in standard form.