Answer:
The required probability is 88% or 0.88
Explanation:
Consider the provided table.
Let X represents the number of children spend at least 1 hour/day outside and number of children spend less than 1 hour/day on electronics respectively.
The total number of children that spend at least an hour a day outside is 16.
Probability of a child spends at least 1 hour per day outside is:
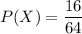
Total number of children who spend less than 1 hour/day on electronics and spend at least 1 hour per day outside = 14
Probability of a child spends less than 1 hour per day on electronics and at least 1 hour per day outside is:
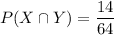
According to conditional probability:
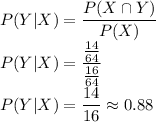
Hence, the required probability is 88% or 0.88