Question

Let ​ f(x)=x2−18x+157 ​.

What is the vertex form of f(x)?

What is the minimum value of f(x)?

Enter your answers in the boxes.
Vertex form: f(x)=

Minimum value of f(x): y =

Answer 1

hello :
f(x)=x²−18x+157
= x²-2(9)(x) +9²-9²+157
= (x-9)² -9²+157
f(x) = (x-9)²+76....(the vertex form of f(x) )
Minimum value of f(x): y = 76

Answer 2

a) The vertex form is
`f(x)=(x-9)^2+76`

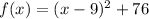
b) The minimum value is 76.

Explanation:

Given : function
`f(x)=x^2-18x+157`

We have to find the vertex form of f(a) and minimum value of f(x).

To write the vertex form.

Consider the given function
`f(x)=x^2-18x+157`

Vertex form a quadratic function
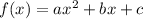`f(x)=ax^2+bx+c` is
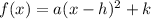`f(x)=a(x-h)^2+k`where (h,k) is the vertex.

We write the square term in perfect square form that is in the form of
`(a-b)^2=a^2+b^2-2ab`

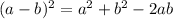
Comparing we have a = x

-2ab = -18x

⇒ b = 9

Add and subtract
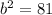`b^2=81` in the given equation, we have,

`f(x)=x^2-18x+81-81+157`

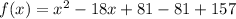
Simplify, we have,

`f(x)=(x-9)^2+76`

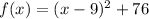
Thus, The vertex form is
`f(x)=(x-9)^2+76`

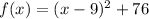
b)

Minimum value of f(x) is at y value of vertex equation.

That is when x = 9 then value of function is
`f(x)=(9-9)^2+76=76`

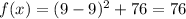
Thus, The minimum value of given function
`f(x)=x^2-18x+157` is 76.