Question

Where is the removable discontinuity of f(x)= x+5/x^2+3x-10

x= -5
x= -2
x= 2
x= 5

Answer 1

The removable discontinuity of f(x) is at x=-5.

Explanation:

A rational function
`f(x)=(p(x))/(q(x))` will have the discontinuity at x=a if q(a)=0. The discontinuity is removable when p(a)=0.

Given the function:
`f(x)=(x+5)/(x^2+3x-10)`

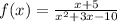
The discontinuity of the function f(x) occurs at the zeros of the denominators
`x^2+3x-10`:

`x^2+3x-10`=0

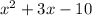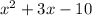`(x+5)(x-2)`=0

⇒ x=2 ,-5.

When x=2 we have the numerator x+5 is

x+5=2+5=7≠0

when x=-5, then the numerator is

x+5=-5+5=0.

Thus, the function f(x) has a removable discontinuity at x=-5.

Answer 2

Rational functions are discontinuous where the denominator is equal to zero. If f(x)=(x+5)/(x^2 + 3x -10), we need to find where x^2 + 3x -10 = 0.
Lets factor the denominator: (x+5)(x-2). So the denominator is 0 in x=-5 and x=2. Nominator is also 0 in x=-5. So we have a hole in x=-5 because the numerator and the denominator are both zero at x=-5 and a vertical asymptote in x=2. The hole is removable discontinuity so the correct answer is x=-5.