Question

Cobalt – 60 used in cancer therapy, decays by beta and gamma emission. The decay constant is 4.18x10 -9 /s. What is the half-life in years?

Answer 1

The decay constant ( λ) tells us the probability of a radioactive nuclide in time. We can relate the decay constant to the half-life of the nuclide by the following equation:

`t_{(1)/(2)}=(ln2)/(\lambda)`

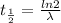
Where λ is the decay constant and t1/2 is the half-life time

We replace the value of λ and we find the half-life time

`t_(1/2)=(ln2)/(4.18*10^(-9)/s)`
`t_(1/2)=1.66*10^8s*(1year)/(3.154*10^7s)=5.26years`

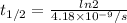
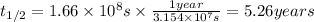
The half-time of Cobalt-60 is 5.26 years

Answer: 5.26 years