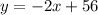Question

What is the equation for the linear model in the scatter plot obtained by choosing the two points closest to the line?

A)Y = -3 x+ 56
B)Y = -2 x +46
C)Y = -2 x +56
D)Y = 2 x + 56

Answer 1

The best choice would probably be C. We know the y-intercept is higher than 46 and that the slope is negative. That leaves us with choice A and C. We can eliminate A because when using the slope formula, the answer is closer to 2 than 3. However, even though it's most likely C, I would check first.

Answer 2

Option C is the answer.

Explanation:

To find the equation of the straight line equation i.e, we must be given with the two points
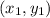`\left (x_(1),y_(1) \right )` and
`\left (x_(2),y_(2)\right )`

Since from the graph the two points closest to the line are
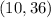`\left ( 10,36 \right )` and
`\left ( 22,12 \right ).`

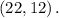
Equation of line with two points closest to the line :

`y-y_(1)=m\cdot \left ( x-x_(1) \right )`

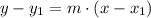
where m is the slope.

First we find the slope(m)=
`(y_(2)-y_(1))/(x_(2)-x_(1))`

`m=(12-36)/(22-10)`

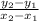
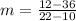
on simplify we get,
`m=-2`.

Now, to find the equation of the line:
`y-y_(1)=m\cdot \left ( x-x_(1) \right )`

`y-36=\left ( -2 \right )\cdot \left ( x-10 \right )`

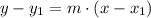
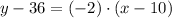
Apply distributive property on right hand side, we get

`y-36=-2\cdot x+20`

Adding both sides by 36, we get

`y=-2x+20+36`

`y=-2x+56`.

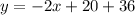
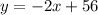The equation for the linear model in the scatter plot obtained by the two closest point
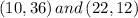`\left ( 10,36 \right ) and \left ( 22,12 \right )` closest to the line is,

`y=-2x+56`