Question

Which ordered pair makes both inequalities true?

y > –3x + 3
y > 2x – 2
(1,0)

(–1,1)

(2,2)

(0,3)

Answer 1

(2,2).

Explanation:

The given inequalities are

`y>-3x+3`

`y>2x-2`

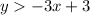
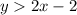
To answer this question, we just have to replace each pair and see which one makes these inequalities true.

For
`(1,0)`

`y>-3x+3\\0>-3(1)+3\\0>-3+3\\0>0`

`y>2x-2\\0>2(1)-2\\0>2-2\\0>0`

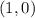
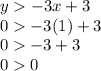
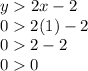
For
`(-1,1)`

`y>-3x+3\\1>-3(-1)+3\\1>3+3\\1>6`

`y>2x-2\\1>2(-1)-2\\1>-2-2\\1>-4`

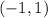
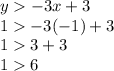
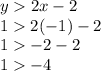
For
`(2,2)`

`y>-3x+3\\2>-3(2)+3\\2>-6+3\\2>-3`

`y>2x-2\\2>2(2)-2\\2>4-2\\2>2`

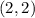
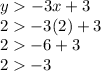
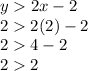
For
`(0,3)`

`y>-3x+3\\3>-3(0)+3\\3>3`

`y>2x-2\\3>2(0)-2\\3>-2`

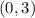
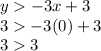
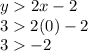
Now, if we graph, we could get the right answer, because with these results the answer is not clear.

In the graph, you could see that (2,2) (1,0) and (0,3) could answers here, because all three of them present the same characteristic, they are in the edge of the shaded area.

However, when we have inequality system problems, those which have a null coordinate don't apply for solution.

Therefore, the best answer is (2,2).