Answer:
The final temperature of the mixture = 79.4°C
Step-by-step explanation:
Mass of water, mw = 130g = 130/1000
mw = 0.13 kg
Initial temperature of the water, θw = 97°C
Let the final temperature of the mixture be θ
Specific capacity of water, cw = 4200 J/kg°C
Heat lost by the water
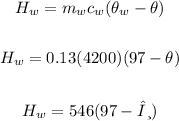
Mass of the noodles, mn = 86 g
mn = 86/1000 = 0.086 kg
Specific capacity of the noodles, cn = 1700 J/kg°C
Initial temperature of the noodles, θn = 20°C
Heat gained by the noodles
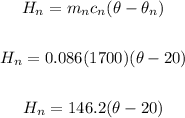
Mass of the seasoning, ms = 12 g
ms = 12/1000 = 0.012 kg
Specific capacity of the noodles, cs = 1300 J/kg°C
Initial temperature of the noodles, θs = 20°C
Heat gained by the seasoning
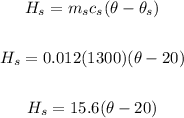
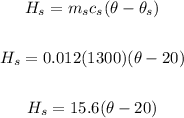
Heat lost by the water = Heat gained by the noodles + Heat gained by the seasoning

The final temperature of the mixture = 79.4°C