Answer:
The correct option is 3.
Explanation:
The given function is
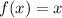 if 0 ≤ x ≤ 4
if 0 ≤ x ≤ 4
where x is the greatest integer function.
This function can be written as
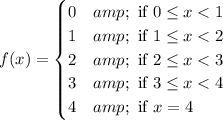
It means the values of the function is 0 in the interval 0≤x<1, 0 in the interval 0≤x<1, 1 in the interval 1≤x<2, 2 in the interval 2≤x<3, 3 in the interval 3≤x<4, 4 at x=4.
From these interval in is clear that the closed circle in on the left side of the floor and open circle on the right side on each floor.
Therefore the correct option is 3.