Answer:
Option B - 3.75 mg
Explanation:
Given : Polonium-218 has a half-life of about 3 minutes.
To find : After 15 minutes, how many milligrams of a 120 mg sample will remain?
Solution :
Considering an exponential model,
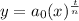
Where, y is the total amount
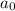 is the original amount
is the original amount
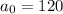
x is the half-life of Polonium-218
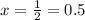
t is the time taken t=15 minutes
n is the time spent n=3 minutes
Substitute the values in the exponential model,
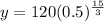
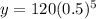
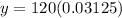
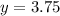
Therefore, Option B is correct.
3.75 mg is required amount.