Question

Help asap

Simplify completely quantity 8 x minus 16 over quantity x squared minus 13 x plus 22 and find the restrictions on the variable.
quantity x minus 2 over quantity x minus 11, x ≠ 11
quantity x minus 2 over quantity x minus 11, x ≠ 2, x ≠ 11
8 over quantity x minus 11, x ≠ 11
8 over quantity x minus 11, x ≠ 2, x ≠ 11

Answer 1

1) (8x-16) / (x²-13x+22) = (8x-16) / (x-11)(x-2)= 8(x-2)/(x-11)(x-2) = 8/(x-11)
Restriction x ≠ 11 & x ≠ 2

Since both values render the denominator = to Zero & we can't divide by 0

Answer 2

Answer: The correct option is last, i.e., 8 over quantity x minus 11, x ≠ 2, x ≠ 11.

Step-by-step explanation:

The given expression is,

`(8x-16)/(x^2-13x+22)`

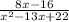
Use factoring method to factorise the denominator.

`(8x-16)/(x^2-13x+22)=(8(x-2))/(x^2-11x-2x+22)`

`(8x-16)/(x^2-13x+22)=(8(x-2))/(x(x-11)-2(x-11))`

`(8x-16)/(x^2-13x+22)=(8(x-2))/((x-11)(x-2))`

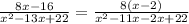
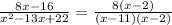
The factors of denominator are (x-11) and (x-2), therefore the function is not defined for x=11 and x=2.

Cancel out the common factor (x-2).

`(8x-16)/(x^2-13x+22)=(8)/(x-11)`

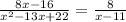
Therefore, the simplified form of the given expression is 8 over quantity x minus 11, x ≠ 2, x ≠ 11, So the last option is correct.