To find the probability of selecting four students that are not juniors, we must find the number of students who are not juniors in each class. So, we have
First class = 15 - 9 = 6
Second class = 15 - 12 = 3
Third class = 15 - 6 = 9
Fourth class = 15 - 3 = 12
Thus, for each class, we can get the probability that the selected student is not a junior as shown below.
First class = 6/15
Second class = 3/15
Third class = 9/15
Fourth class = 12/15
To find the probability of selecting four students that are not juniors, we multiply the probabilities from the four classes.
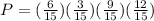
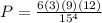
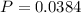
Thus, Mrs Bergstedt has a probability of 0.0384 of selecting four students that are not juniors.
Answer: 0.0384